Metapoblaciones - 3.2
Published:
Destrucción del hábitat y metapoblaciones
Una de las aplicaciones más importantes de los modelos de metapoblaciones es estudiar la persistencia de una especie, el riesgo de extinción, o como hacer para eliminar una especie plaga.
Uno de los problemas producidos por el hombre es la destrucción del hábitat
Esto puede agregarse al modelo de Levins como una proporción de parches destruidos $D$
$\dfrac{dp}{dt} = m p (1 - p - D) - \gamma p$
$\dfrac{dN}{dt} = m N (1 - \dfrac{N}{T} - DT) - \gamma N$
La ocupación en el equilibrio sería entonces:
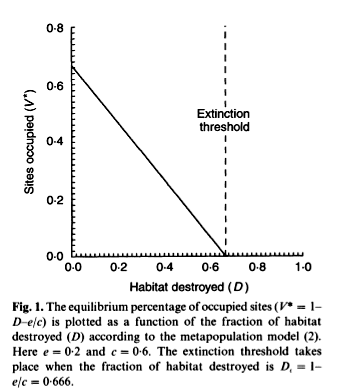
$p^*=1-D-\gamma/m$
Un resultado importante es que existe un valor crítico para el cual la metapoblacion se extingue a pesar de que existen parches disponibles:
$D_c=1-\gamma/m$
Un extensión sería tener en cuenta que la colonización no se produce desde todos los parches sino lo más probable es que suceda desde el parche más cercano.
Una forma de hacer esto es utilizando un modelo IBM espacialmente explícito, estos modelos son llamados sistemas de partículas interactivas (interactive particle systems). Para simplificar ponemos los parches en una grilla y tenemos $T=dimx \times dimy$,
Los parches ocupados se extinguen a una tasa $\gamma$, cuando decimos que un evento sucede a una tasa $\gamma$ significa que el tiempo entre sucesivas eventos $\tau_i$ tiene una distribución exponencial con parámetro $\gamma$, lo cual es igual a: $P(\tau_i \le t )= 1 - exp(-\gamma t)$
Los parches vacíos tiene una probabilidad $m \rho$ de ser colonizados siendo $\rho$ la proporción de parches ocupados en el entorno
Para evaluar el modelo en tiempo continuo se toma al azar un parche y se evalúa con las transiciones con probabilidad $\gamma/R$ o $m/R$
Empecemos implementando este modelo en R
dimx <- 10
dimy <- 10
pa <- matrix(rbinom(dimy*dimx,1,0.5),dimy,dimx)
m <- 0.6
g <- 0.2
R <- m+g
m <- m/R
g <- g/R
eval_parche <-function(r,c,m,g){
rp1 <- ifelse(r>=dimx,1,r+1)
rm1 <- ifelse(r==1,dimx,r-1)
cp1 <- ifelse(c>=dimy,1,c+1)
cm1 <- ifelse(c==1,dimy,c-1)
y <- runif(1)
if(pa[r,c]==0){
C <-(pa[rp1,c]+pa[rm1,c]+pa[r,cp1]+pa[r,cm1])/4 * m
if(y<=C)
pa[r,c] <<- 1
} else {
if(y<=g)
pa[r,c] <<- 0
}
}
- Esta función sirve para evaluar 1 parche, si queremos evaluar todos los parches podemos usar repeat
sim_parches <- function(m,g){
R <- m+g
m <- m/R
g <- g/R
nsim <-0
tsim <- dimx*dimy*R
repeat{
r <- sample.int(dimy,1)
c <- sample.int(dimx,1)
eval_parche(r,c,m,g)
nsim <-nsim +1
if(nsim>tsim)
break
}
}
- Esta función evalúa 1 solo paso temporal
image(pa,asp=1,axes=F,col=c("white","blue"))
sim_parches(.6,.2)
image(pa,asp=1,axes=F,col=c("white","blue"))
- Nos falta agregar el time
sim_parches <- function(time,m,g){
R <- m+g
m <- m/R
g <- g/R
t <- 0
tsim <- dimx*dimy*R
repeat{
nsim <-0
repeat{
r <- sample.int(dimy,1)
c <- sample.int(dimx,1)
eval_parche(r,c,m,g)
nsim <-nsim +1
if(nsim>tsim)
break
}
t <- t+1
image(pa,asp=1,axes=F,col=c("white","blue"),useRaster = TRUE)
if(t>time)
break
}
}
sim_parches(10,.6,.2)
- Habría que agregar un parámetro para que no grafique el estado de los parches
sim_parches <- function(time,m,g,plt=FALSE){
...
t <- t+1
if(plt) image(pa,asp=1,axes=F,col=c("white","blue"),useRaster = TRUE)
...
}
sim_parches(10,.6,.2)
- Toda la informacion del modelo esta en la matriz pa, para reiniciar la simulacion tenemos que asignar nuevamente valores a pa
source("Meta_fun.r")
dimx <- 10
dimy <- 10
pa <- matrix(rbinom(dimy*dimx,1,0.5),dimy,dimx)
sim_parches(10,.6,.2)
- Pero siempre calculamos sobre la misma matriz, por lo que no tenemos la cantidad de parches ocupados en el tiempo. Deberíamos calcularlo y guardarlo en un vector.
sim_parches <- function(time,m,g,plt=FALSE){
p <- numeric(time)
R <- m+g
m <- m/R
g <- g/R
t <- 0
tsim <- dimx*dimy*R
repeat{
nsim <-0
repeat{
r <- sample.int(dimy,1)
c <- sample.int(dimx,1)
eval_parche(r,c,m,g)
nsim <-nsim +1
if(nsim>tsim)
break
}
t <- t+1
if(t>time)
break
if(plt) image(pa,asp=1,axes=F,col=c("white","blue"),useRaster = TRUE)
p[t]<- sum(pa)
}
return(p)
}
sim_parches(100,.6,.2)
sim_parches(100,.6,.5)
- lo último que nos faltaría hacer para que quede bien definida la función de simulación es que utilice una matriz propia y la inicialice, para eso no hay otra forma de hacerlo que eliminando la función eval_parche.
sim_parches <- function(dimx,dimy,pIni,time,m,g,plt=FALSE){
p <- numeric(time)
pa <- matrix(rbinom(dimy*dimx,1,pIni),dimy,dimx)
R <- m+g
m <- m/R
g <- g/R
t <- 0
tsim <- dimx*dimy*R
repeat{
nsim <-0
repeat{
r <- sample.int(dimy,1)
c <- sample.int(dimx,1)
# eval_parche
rp1 <- ifelse(r>=dimx,1,r+1)
rm1 <- ifelse(r==1,dimx,r-1)
cp1 <- ifelse(c>=dimy,1,c+1)
cm1 <- ifelse(c==1,dimy,c-1)
y <- runif(1)
if(pa[r,c]==0){
C <-(pa[rp1,c]+pa[rm1,c]+pa[r,cp1]+pa[r,cm1])/4 * m
if(y<=C)
pa[r,c] <- 1
} else {
if(y<=g)
pa[r,c] <- 0
}
# fin eval_parche
nsim <-nsim +1
if(nsim>tsim)
break
}
t <- t+1
if(t>time)
break
if(plt) image(pa,asp=1,axes=F,col=c("white","blue"),useRaster = TRUE)
p[t]<- sum(pa)
}
return(p)
}
- La función está cargada en el archivo Meta_fun.r del google drive.
# borramos las variables locales para estar seguros que no se mezclan
#
rm(pa,dimx,dimy)
source("Meta_fun.r")
p <-sim_parches1(30,30,.5,100,.6,.3,10)
Cuales son las consecuencias de hacer el modelo espacialmente explícito?
$p^*=1-\gamma/m$
mean(p)
plot(levins(100,.5,.6,.3)*900,col="red",xlab="Tiempo",ylab="N")
points(p,col="chocolate")
points(levins_IBM(100,450,.6,.3,900),col="orange")
Referencias
Keymer JE, Marquet PA, Velasco-Hernández JX, Levin SA (2000) Extinction Thresholds and Metapopulation Persistence in Dynamic Landscapes. Am Nat 156: 478–494. https://drive.google.com/file/d/0BzexxHVKtpiAd0VjSWdTSmZBd1k/view?usp=sharing
Bascompte J, Sole R V (1996) Habitat Fragmentation and Extinction Thresholds in Spatially Explicit Models. J Anim Ecol 65: 465. doi:10.2307/5781. https://drive.google.com/file/d/0BzexxHVKtpiANkJqTVo3M3BLZTA/view?usp=sharing
Ross J V (2006) Stochastic models for mainland-island metapopulations in static and dynamic landscapes. Bull Math Biol 68: 417–449. doi:10.1007/s11538-005-9043-y. < https://drive.google.com/file/d/0BzexxHVKtpiAWXNzaFFiMXNabk0/view?usp=sharing>
Renshaw E (1993) Modelling biological populations in space and time. Cambridge University Press. Cap 7 https://drive.google.com/file/d/0BzexxHVKtpiAYTNMNlQ2b2o2c1k/view?usp=sharing
Black AJ, McKane AJ (2012) Stochastic formulation of ecological models and their applications. Trends Ecol Evol 27: 337–345. doi:10.1016/j.tree.2012.01.014.https://drive.google.com/file/d/0BzexxHVKtpiAY05KZnJpMC10SWM/view?usp=sharing
Henry SM (2009) A Primer of Ecology with R. Springer. https://drive.google.com/file/d/0BzexxHVKtpiAVlhfLWRiS2d4aWM/view?usp=sharing
Crawley MJ (2012) The R Book. 2nd Edition. Wiley. https://drive.google.com/file/d/0BzexxHVKtpiAaGJwMng5WTNveEk/view?usp=sharing
Bolker B (2008) Ecological Models and Data in R. Princeton University Press. https://drive.google.com/file/d/0BzexxHVKtpiAQjhBRDdZQW51WlU/view?usp=sharing

Leave a Comment