Fractals in time - Day 2

Characteristic features of fractals

• Mandelbrot Originally defined fractals as sets that have fractal dimension strictly greater than its topological dimension.

• There is no hard and fast definition but a list of properties.

• We refer to F as fractal if:

  1. F has a fine structure: i.e. detail on small scales.

  2. F is too irregular to be described by traditional geometrical language

  3. F has some form of self-similarity, perhaps approximate or statistical

  4. Usually the fractal dimension of F is greater than its topological dimension

Random walks

• Random walk (RW) is a stochastic process in which an object moves in a space by performing random jumps

  

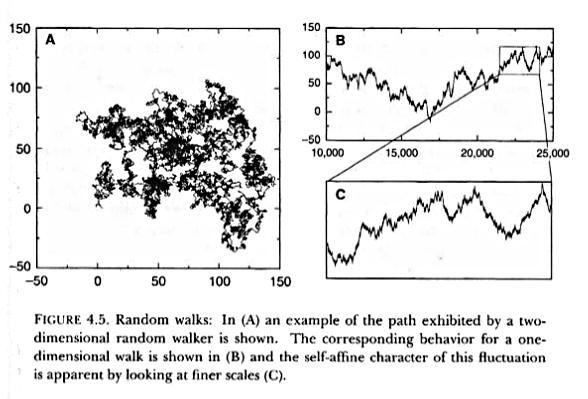
• We can see that the enlarged view of a small part of the trajectory looks similar to the original, is fractal.

• The pattern displayed by the one dimensional RW is not self-similar but self-affine because the time and space dimensions do not scale in the same way

Fractal time series

• Fractal properties in time series can be analyzed by means of Hurst’s Rescaled Range Analysis

  Let us consider a time series that can be: the number of extinctions of a group of organism or a particular population or the discharge of a river, etc.

  $X_i$ with $i=1,2,3,…,T$

  The average of $X_i$ over $T$ time steps will be $< X >T = \left( \sum{i} X_t \right)/T$

  The departure from the average over a t-year time horizont is given by:

  $$X(t,T) = \sum_{i=1}^{t} [X_i - < X >T ] = \left( \sum{i=1}^{T} X_i \right) - t < X >_T$$

  $X(t,T)$ is usually calculated dividing the time series in $M$ segments of size $T$.

• What is the value of $X(T,T)$ ?

Rescaled Range Analysis

• We need to calculate two more quantities from the previous :

  The standard deviation $S(T) = \left( (< X_t - < X >_T >)^2 \right)^{1/2}$

  The range $R(T) = \max_{1 \le t \le T} X(t,T) - \min_{1 \le t \le T} X(t,T)$

• The rescaled range is: $F(T)=R(T)/S(T)$

• Calculate $F(T)$ using $T=5$ and the following series

    3  4  9  2  1  7  8  2  2  9 
  

• When the values of the time series are uncorrelated $F(T) \propto T^{1/2}$, which is called white noise. The best predictor is the last measured value.

• Hurst found a more general scaling relation $F(T) \propto T^{H}$.

  for the natural systems he analyzed $H > 1/2$

  it can be shown (easily) than the fractal dimension is related:

  $$D = 2 - H$$

• When the Hurst exponent is greater than 1/2 the system shows persistence on all time scales. An increasing trend in the past implies an increasing trend in the future.

  If $H < 1/2$ an increase in the past implies a decrease in the future, the system shows antipersistence.

Papers

We will analyze the data from the paper:

1. Meltzer MI, Hastings HM (1992) The use of fractals to assess the ecological impact of increased cattle population: case study from the Runde Communal Land, Zimbabwe. Journal of Applied Ecology 29: 635–646.