Metapoblaciones - 2.1
Published:
Un modelo mínimo de metapoblaciones: dos parches
$\dfrac{dn_1}{dt} = n_1 r_1 (1 - \frac{n_1}{k_1}) - \epsilon n_1 + \epsilon n_2$
$\dfrac{dn_2}{dt} = n_2 r_2 (1 - \frac{n_2}{k_2}) - \epsilon n_2 + \epsilon n_1$
Isolineas de crecimiento cero - Nullclines
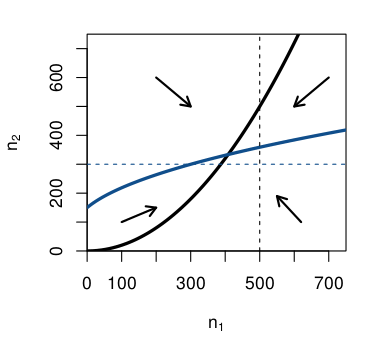
Negro: isolínea $n_1$, azul:isolínea $n_2$. Las líneas de puntos son las capacidades de carga.
Puesto que los tamaños de las poblaciones acopladas en equilibrio están dadas por la intersección de las líneas continuas, la dispersión hace que la abundancia en el parche de 1 sea menos de lo que ocurriría si existiera el parche en forma aislada, mientras que la abundancia en el parche 2 es mayor que si existiera el parche en forma aislada.
Las flechas indican la dirección neta que la dinámica tomarán en las cuatro regiones delimitadas por las isolineas. Parámetros utilizados en este ejemplo son $r_1 = 1$, $r_2 = 2$, $k_1 = 500$, $k_2 = 300$, y $\epsilon= 1$.
Funciones en R
Estructura de una función
nombre_de_f <- function(parametros=valorPorDefecto) { # Aca adentro va lo que hace la funcion return("resultado que devuelve la función") }ver página 356 de libro de Henry
Es más facil calcular la trayectoria de las ecuaciones en tiempo discreto
$n_1(t+1) = n_1 + n_1 r_1 (1 - \frac{n_1}{k_1}) - \epsilon n_1 + \epsilon n_2$
$n_2(t+1) = n_2 + n_2 r_2 (1 - \frac{n_2}{k_2}) - \epsilon n_2 + \epsilon n_1$
ver página 366 de Henry para integración de ODE usando deSolve
Patch2 <- function() { n[1] <- n[1] + n[1]*r[1]*(1 - n[1]/k[1]) - e + n[1] + e n[2] n[2] <- n[2] + n[2]*r[2]*(1 - n[2]/k[2]) - e + n[2] + e n[1] }faltan los parámetros
Patch2 <- function(n,r,k,e) { n[1] <- n[1] + n[1]*r[1]*(1 - n[1]/k[1]) - e *n[1] + e*n[2] n[2] <- n[2] + n[2]*r[2]*(1 - n[2]/k[2]) - e *n[2] + e*n[1] }A probar si funciona!!!
n <- Patch2( c(10,10), c(1,2),c(500,300),1) nCómo hacemos para que nos de una trayectoria en el tiempo
Si aún no lo hicieron, conviene crear un script!
Patch2 <- function(time,n,r,k,e){ p1 <- numeric(time) p2 <- numeric(time)
p1[i] <- p1[i-1] + p1[i-1]*r[1]*(1 - p1[i-1]/k[1]) - e *p1[i-1] + e*p2[i-1]
p2[i] <- p2[i-1] + p2[i-1]*r[2]*(1 - p2[i-1]/k[2]) - e *p2[i-1] + e*p2[i-1]
}
}
La función debe devolver algo, le falta el return()
Patch2 <- function(time,n,r,k,e){ p1 <- numeric(time) p2 <- numeric(time)
p1[i] <- p1[i-1] + p1[i-1]*r[1]*(1 - p1[i-1]/k[1]) - e *p1[i-1] + e*p2[i-1]
p2[i] <- p2[i-1] + p2[i-1]*r[2]*(1 - p2[i-1]/k[2]) - e *p2[i-1] + e*p2[i-1]
}
return(list(n1=p1,n2=p2))
}
Patch2(100,c(10,10), c(1,2),c(500,300),1)
Ahora a encontrar el error!
Falta inicializar las p’s
Patch2 <- function(time,n,r,k,e){ p1 <- numeric(time) p2 <- numeric(time) p1[1] <- n[1] p2[1] <- n[2]
p1[i] <- p1[i-1] + p1[i-1]*r[1]*(1 - p1[i-1]/k[1]) - e *p1[i-1] + e*p2[i-1]
p2[i] <- p2[i-1] + p2[i-1]*r[2]*(1 - p2[i-1]/k[2]) - e *p2[i-1] + e*p2[i-1]
}
return(list(n1=p1,n2=p2))
}
Prueben hacer un gráfico con plot
Una forma es:
po <- Patch2(1000,c(10,10), c(1,2),c(500,300),1) plot(po2$n1,po2$n2) plot(po2$n1) points(po2$n2)Para usar ggplot hay que hacer un data.frame
g + theme_bw()da <- data.frame(time=1:1000,n1=po$n1,n2=po$n2) g <- ggplot(da,aes(n1,n2)) + geom_point()Para usar la potencia de ggplot hay que cambiar un poco la organización de los datos
da <- data.frame(time=rep(1:1000,2),n=c(po$n1,po$n2),pob=rep(1:2,each=1000)) g <- ggplot(da,aes(time,n,colour=as.factor(pob))) + geom_point(size=1) g + theme_bw()que tal si nos quedamos con los últimos 100 puntos
da <- da[da$time>=900,] g <- ggplot(da,aes(time,n,colour=as.factor(pob))) + geom_point(size=1) + theme_bw() g g + geom_line() g + geom_smooth()que tal si aumentamos los r’s, y de paso cambiamos la función para que devuelva un data.frame
for(i in 2:time){Patch2 <- function(time,n,r,k,e) { p1 <- numeric(time) p2 <- numeric(time) p1[1] <- n[1] p2[1] <- n[2]p1[i] <- p1[i-1] + p1[i-1]*r[1]*(1 - p1[i-1]/k[1]) - e *p1[i-1] + e*p2[i-1] p2[i] <- p2[i-1] + p2[i-1]*r[2]*(1 - p2[i-1]/k[2]) - e *p2[i-1] + e*p2[i-1] } return(data.frame(time=rep(1:time,2),n=c(p1,p2),pob=rep(1:2,each=1000))) } da <- Patch2(1000,c(10,10), c(2,2.3),c(500,300),1) da <- da[da$time>=900,] g <- ggplot(da,aes(time,n,colour=as.factor(pob))) + geom_point(size=1) + theme_bw() g g + geom_line() g + geom_smooth()
Cómo era eso de la pregunta ecológica/biológica?
Cuales son los supuestos del modelo?
$n_1(t+1) = n_1 + n_1 r_1 (1 - \frac{n_1}{k_1}) - \epsilon n_1 + \epsilon n_2$
$n_2(t+1) = n_2 + n_2 r_2 (1 - \frac{n_2}{k_2}) - \epsilon n_2 + \epsilon n_1$
Qué preguntas nos podemos responder con este modelo?
The effect of dispersal on population size and stability is explored for a population that disperses passively between two discrete habitat patches. Two basic models are considered. In the first model, a single population experiences density-dependent growth in both patches. A graphical construction is presented which allows one to determine the spatial pattern of abundance at equilibrium for most reasonable growth models and rates of dispersal. It is shown under rather general conditions that this equilibrium is unique and globally stable. In the second model, the dispersing population is a food-limited predator that occurs in both a source habitat (which contains a prey population) and a sink habitat (which does not). Passive dispersal between source and sink habitats can stabilize an otherwise unstable predator-prey interaction. The conditions allowing this are explored in some detail… Queda como lectura para la tarde.
Referencias
Henry SM (2009) A Primer of Ecology with R. Springer. https://drive.google.com/file/d/0BzexxHVKtpiAVlhfLWRiS2d4aWM/view?usp=sharing
Crawley MJ (2012) The R Book. 2nd Edition. Wiley. https://drive.google.com/file/d/0BzexxHVKtpiAaGJwMng5WTNveEk/view?usp=sharing
Bolker B (2008) Ecological Models and Data in R. Princeton University Press. https://drive.google.com/file/d/0BzexxHVKtpiAQjhBRDdZQW51WlU/view?usp=sharing

Leave a Comment