Metapoblaciones - 2.2
Published:
El modelo clásico de metapoblaciones
Supuestos: tenemos una población distribuida en parches
La colonización y la extinción de los parches es lenta en comparación con el crecimiento dentro del parche; esto significa que los parches ocupados estarán cerca de la capacidad de carga.
La capacidad de carga promedio entre $T$ parches es $k$
La colonización y la extinción no están relacionadas a las propiedades del parche, ni al tamaño de la población en el parche.
$N$ es el numero de parches ocupados y $p=N/T$ la ocupación de los parches
La extinción de la población por parche es $\gamma$, la tasa total de extinción es $\gamma N$
La producción por parche de individuos que migran para colonizar otros parches es $m$
$\dfrac{dN}{dt} = m N (1 - \dfrac{N}{T}) - \gamma N$
Lo cual puede representarse en términos de la ocupación (fracción de parches ocupados)
$\dfrac{dp}{dt} = m p (1 - p) - \gamma p$
Igualando a 0 tenemos la ocupación en el equilibrio
$p^*=1-\gamma/m$
A menos que la extinción $\gamma=0$ nunca están todos los parches ocupados. Para que la metapoblación persista ($p^*>0$), debe ser $m >\gamma$.
Esto se observaba en el ejemplo de las mariposas
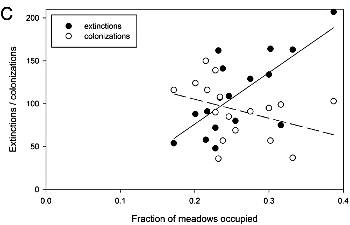
Este gráfico es compatible con las suposiciones?
Hagamos una función en R!
- Es más fácil que la anterior porque tiene que devolver una sola variable
levins <- function(time,n,m,g)
{
p <- numeric(time)
p[1] <-n
for(i in 2:time){
p[i] <- p[i-1] + m*p[i-1]*(1-p[i-1]) - g *p[i-1]
}
return(p)
}
levins(100,.1,.6,.5)
- Podemos hacer una función que calcule la dinámica con distintos valores del parámetro y cree un data.frame para graficar
levins_gamma <- function(time,n,m,g)
{
# g debe ser un vector de dos componentes
dif <- seq(g[1],g[2],length.out=5)
#inicializamos un data.frame vacio
da <- data.frame()
for(i in dif) {
pp <- levins(time,n,m,i)
# tenemos que hacer crecer el data.frame
da <- rbind(da,data.frame(time=1:time,pob=pp,gamma=dif))
}
return(da)
}
- Ejecutamos y graficamos
le <- levins_gamma(100,.1,.6,c(.5,.7))
g <- ggplot(le,aes(time,pob,colour=as.factor(gamma))) + geom_point(size=1) + theme_bw()
g
g + geom_line()
g + geom_smooth()
- Algo anda mal
head(le)
levins_gamma <- function(time,n,m,g)
{
dif <- seq(g[1],g[2],length.out=5)
da <- data.frame()
for(i in dif) {
pp <- levins(time,n,m,i)
da <- rbind(da,data.frame(time=1:time,pob=pp,gamma=i))
}
return(da)
}
Volvemos a ejecutar
le <- levins_gamma(100,.1,.6,c(.5,.7))
head(le)
# parece que anda bien
g <- ggplot(le,aes(time,pob,colour=as.factor(gamma))) + geom_point(size=1) + theme_bw()
g
g + geom_line()
Para que sea más divertido podemos agregarle estocacidad
Esto relaciona los datos de campo/experimentales con el modelo
Hay básicamente dos formas (después vemos la tercera)
Error de observación: no podemos contar todos los individuos en una población, en general se trabaja con muestras. Si asumimos que tenemos una probabilidad $q$ de contar cada individuo eso nos lleva a una distribución binomial (página 168 libro de Bolker)
$u(t+1) = m u(t) (1 - \dfrac{u(t)}{v}) - \gamma u(t)$
$u_{obs}(t) \sim Binomial(u(t),q)$
Hagamos el código para el error de observación
levins_obs <- function(time,n,m,g,q)
{
v <- 1000
p <- numeric(time)
pObs <- numeric(time)
p[1] <-n
pObs[1] <- rbinom(1,round(p[1]),q)
for(i in 2:time){
p[i] <- p[i-1] + m*p[i-1]*(1-p[i-1]/v) - g *p[i-1]
pObs[i] <- rbinom(1,round(p[i]),q)
}
return(list(pob=p,pObs=pObs))
}
# Ojo acá tenemos que pasar el n inicial como número de individuos
levins_obs(100,10,.6,.5,0.8)
- Para completar el asunto hagamos la función para graficar
levinsObs_gamma <- function(time,n,m,g,q)
{
dif <- seq(g[1],g[2],length.out=5)
da <- data.frame()
for(i in dif) {
pp <- levins_obs(time,n,m,i,q)
da <- rbind(da,data.frame(time=1:time,pob=pp$pob,pObs=pp$pObs,gamma=i,q=q))
}
return(da)
}
Simulamos
le <- levinsObs_gamma(200,10,.6,c(.5,.7),.8)
head(le)
g <- ggplot(le,aes(time,pob,colour=as.factor(gamma))) + geom_point(size=1) + theme_bw()
g
g + geom_point(aes(time,pObs),shape=8,size=1)
Si prueban cambiando el parámetro v=100 (dentro de la función), o el parametro q…
Nos falta ver el Error de proceso: el número de individuos fluctúa debido a factores estocásticos. Entonces suponemos una distribución de Poisson (página 171 de Bolker)
$u(t+1) \sim Poisson(m u(t) (1 - \dfrac{u(t)}{v}) - \gamma u(t))$
$u_{obs}(t) = u(t)$
Hacemos la función para error de proceso:
# le agrego como parámetro la cantidad total de parches v
#
levins_pro <- function(time,n,m,g,v)
{
p <- numeric(time)
#pObs <- numeric(time)
p[1] <-rpois(1,n)
#pObs[1] <- rbinom(1,round(p[1]),q)
for(i in 2:time){
p[i] <- rpois(1,p[i-1] + m*p[i-1]*(1-p[i-1]/v) - g *p[i-1])
}
return(p)
}
# Ojo acá tenemos que pasar el n inicial como número de individuos
levins_pro(100,10,.6,.5,1000)
Para ver como cambia habría que comparar distintas simulaciones con los mismos parámetros, y luego con el modelo determinista y con el de error de medición.
- Just do it!
Para algunas otras cosillas de simulación y estimación ver página 454 libro de Bolker.
Para más sobre el modelo de Levins leer el original:
Levins R (1969) Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull Entomol Soc Am 15: 237–240. https://drive.google.com/file/d/0BzexxHVKtpiAc1NnMVY3ZUVSYms/view?usp=sharing
Referencias
Henry SM (2009) A Primer of Ecology with R. Springer. https://drive.google.com/file/d/0BzexxHVKtpiAVlhfLWRiS2d4aWM/view?usp=sharing
Crawley MJ (2012) The R Book. 2nd Edition. Wiley. https://drive.google.com/file/d/0BzexxHVKtpiAaGJwMng5WTNveEk/view?usp=sharing
Bolker B (2008) Ecological Models and Data in R. Princeton University Press. https://drive.google.com/file/d/0BzexxHVKtpiAQjhBRDdZQW51WlU/view?usp=sharing

Leave a Comment