Leonardo A. Saravia

Leonardo A. Saravia

I am a professor/researcher of biology/ecology at UNGS

Metapoblaciones - 3.1

Published:

Modelo de Levins estocástico con Error de proceso

  • Función para graficar

source("Meta_fun.r")

levinsPro_sim <- function(time,n,m,g,v,sim=5)
{
	da <- data.frame()

	for(i in 1:sim) {
	  
	  pp <- levins_pro(time,n,m,g,v)
	  
	  da <- rbind(da,data.frame(time=1:time,pob=pp,sim=i,tipo="pro"))
	}

 	pp <- levins(time,n/v,m,g)*v
	  
  	da <- rbind(da,data.frame(time=1:time,pob=pp,sim=i+1,tipo="det"))

	return(da)
}

Simulamos


le <- levinsPro_sim(500,10,.6,.5,1000)

head(le)

g <- ggplot(le,aes(time,pob,colour=as.factor(sim))) + geom_point(size=1) + theme_bw()

g 

g + geom_line()

Las suposiciones del modelo de Levins

  • Tenemos $T$ parches iguales

  • Siempre que un migrante arriba a un parche la colonización es exitosa, con esto la tasa de colonización es proporcional al número de parches ocupados $N$.

  • La tasa total de colonización es $C=m N (1 - \dfrac{N}{T})$

  • La tasa de total de extinción también es proporcional al número de parches ocupados $E= \gamma N$

  • Estas suposiciones dejan de lado procesos biológicos:

    • Puede tomar mas de un migrante para que se establezca una nueva sub-población con lo cual la tasa de colonización podría tener una relación no lineal con la de migración: el efecto Allee.

    • El flujo de migrantes también puede modificar la extinción de una sub-población: el efecto rescate.

Modelo de Levins generalizado

  • Harding KC, McNamara JM (2002) A unifying framework for metapopulation dynamics.

  • Definimos la tasa de colonización por parche $C_{patch}(\alpha)$ y la tasa de extinción por parche $E_{patch}(\beta)$

  • Donde $\alpha$ es la tasa de llegada de colonizadores en un parche vacío y $\beta$ la tasa de llegada de colonizadores a un parche ocupado, estas tasas dependen del número de parches ocupados $N$. El número total de parches lo llamamos $T$

  • Entonces

    $C_{tot}(N)= (T-N)C_{patch}(\alpha(N))$

    $E_{tot}(N)= N E_{patch}(\beta(N))$

    $\dfrac{dN}{dt} = C_{tot}(N) - E_{tot}(N)$

  • Si ponemos $\alpha= \beta=m N/T$ asumimos que los colonizadores se dispersan al azar, con $C_{patch}(\alpha)=\alpha$ y $E_{patch}(\beta)=\gamma$ recuperamos el modelo clásico.

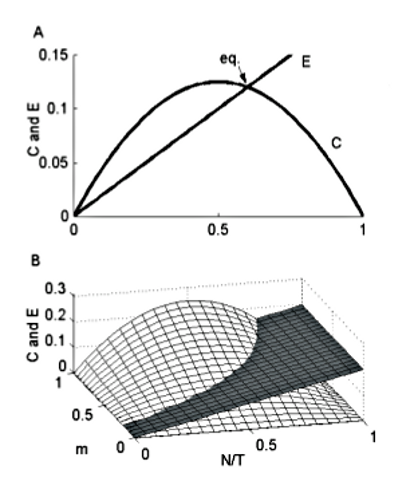
  • Efecto rescate: La contribución de los migrantes a una subpoblación pequeña puede reducir el riesgo de extinción.

    • $E_{patch}(\beta)=\dfrac{\gamma}{1+A\beta}$

    • reemplazamos $E_{tot}(N)= N \dfrac{\gamma}{1+A m N/T}$

    • Graficamos usando R

m <- 0.6

g <- 0.4

curve(x*g,0,1)

curve(x*g/(1+m*x),0,1,add=T,col="red")

curve(m*x*(1 - x),0,1,add=T,col="purple")

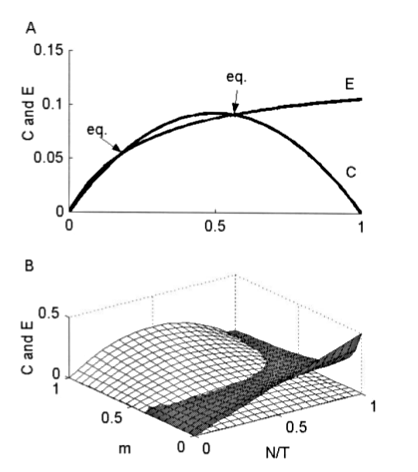
    • Una mayor inmigración puede reducir la endogamia
    • Disminuir las fluctuaciones estocásticas.
    • Aunque también podría aumentar la transmisión de una peste.

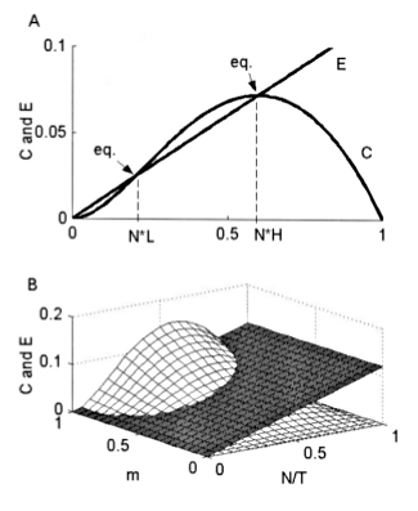
  • Efecto Allee: Puede ser difícil establecerse en un nuevo parche debido a estocacidad demográfica, o complicaciones genéticas cuando el número de individuos es bajo.

    • Entonces $C_{patch}(\alpha)=\alpha$ no sería válido.

    • Típicamente se utiliza una función en forma de S: $C_{patch}(\alpha)=\alpha^2/(\alpha^2+y^2)$

    • Graficar esta curva en R

Qué modelo usarían para las mariposas Melitaea cinxia?

Distintos tipos de estructuras espaciales en las metapoblaciones

  • Hasta ahora pensamos que los parches eran todos iguales en hábitat y tamaño.

  • Isla - continente: en este caso hay una población muy grande que tiene prácticamente riesgo nulo de extinguirse y poblaciones pequeñas que reciben la migración principalmente del continente.

  • Fuente - sumidero: los parches tienen distinta calidad de hábitat, en algunos de ellos no son aptos para contener una población permanente.

  • Definición restringida de metapoblaciones:

    • Cada parche debe soportar una población que se reproduce.
    • Todas las subpoblaciones deben ser propensas a extinguirse.
    • La recolonización debe ser posible.
    • Las dinámicas de las subpoblaciones son asincrónicas

  • Poblaciones en parches: un conjunto de parches conectados por una alta migración, no se producen extinciones locales (efecto rescate) y no hay estructura genética, la población es panmíctica.

  • La estructura de metapoblaciónes así definida no sería tan común en la naturaleza Fronhofer 2012 Why are metapopulations so rare?.

Modelos estocásticos basados en el individuo

  • Los modelos con error de proceso tienen en cuenta la estocacidad demográfica pero son en tiempo discreto.

  • Los modelos basados en el individuo (IBM) tienen en cuenta un número finito de individuos y las reglas para la dinámica son probabilísticas, en forma de procesos de Markov. (La probabilidad de una transición depende solamente del estado actual del sistema)

  • Esto da como resultado la llamada ecuación maestra (ecuación de Kolmogorov hacia adelante)

  • Los IBM se pueden simular de forma exacta, y también se pueden derivar la ecuaciones diferenciales haciendo $N \to \infty$

  • Cuando la población es grande pero aun finita la dinámica puede ser fuertemente estocástica.

  • La ecuación maestra se define calculando la distribución de probabilidades para $N$. Siendo $p_N(t)$ la probabilidad de tener $N$ individuos a tiempo $t$ y $h$ un intervalo de tiempo pequeño.

    1. $Pr[N(t+h)=N(t)+1] = C[N(t)]h$

    2. $Pr[N(t+h)=N(t)-1] = E[N(t)]h$

    3. $Pr[N(t+h)=N(t)] = 1-{C[N(t)]+E[N(t)]}h$

  • entonces

$\begin{multline} p_N(t+h) = p_{N+1}(t) E(N+1))h \

  • p_N(t)[1-{C(N)+E(N)}h] \

  • p_{N-1}(t) C(N-1)h \end{multline}$

  • Dividimos ambos términos por $h$ y haciendo $h \to 0$ nos da la ecuación maestra:
\[\begin{multline} dp_N(t)/dt = E(N+1) p_{N+1}(t) \\ - {C(N)+E(N)} p_N(t) \\ + C(N-1) p_{N-1}(t) \end{multline}\]

Simulación estocástica basada en el individuo

  • El algoritmo es el siguiente:

    1. Especificar Funciones $C(N)$ y $E(N)$, $R(N)=C(N)+E(N)$
    2. Generar dos números al azar $Y_1$ e $Y_2$
    3. Si $Y_1<=C(N)/R(N)$ el próximo evento es nacimiento, sino una muerte.
    4. evaluar el tiempo inter-evento $s = -[log(Y_2)]/R(N)$
    5. Cambiar $N \to N+1$ (Nacimiento/colonización) o $N \to N-1$ (Muerte/Extinción)
    6. volver al paso 2

  • Vamos a usar estructuras de control de flujo en R


if(condicion) {

	acciones si la condicion es verdadera

} else {

	acciones si la condicion es falsa
}

# 
repeat{

	if(condicion) {

		break

	}

}
  • Asumimos las funciones clasicas de Levins


levins_IBM <- function(time,n,m,g,v)
{
	p <- numeric(time)

	p[1] <-rpois(1,n)

    # inicializar variables
    pAnt <- p[1]	
	i <-2
	s <-1
	repeat{

		C <- m*pAnt*(1-pAnt/v) 
		E <- g *pAnt
		R <- C+E
		y <- runif(2)
		if( y[1]<=C/R) 
			pAnt <- pAnt+1
		else
			pAnt <- pAnt-1
		s <- s + (-log(y[2]))/R
		if(s>=i)
		{
			p[i] <- pAnt
			i<- i+1
			if(i>time)
				break
		}
	}

	return(p)
}

levins_IBM(500,10,.6,.5,1000)

# Si hay un error podemos utilizar la funcion debug

debug(levins_IBM)



lo mejor es guardar la funcion en un archivo .r y utilizar el debug de RStudio


source("Meta_fun.r")

le <- levinsIBM_sim(500,10,.6,.5,1000)

head(le)

g <- ggplot(le,aes(time,pob,colour=as.factor(sim))) + geom_point(size=1) + theme_bw()

g 

g + geom_line()

Ejercicio

  • Cuan distintos tienen que ser los parametros del modelo para poder detectar distintas dinámicas metapoblacionales?

  • Hacemos una funcion similar a las que hicimos para los otros modelos

# Simulaciones con Levins IBM y Levins deterministico
#
#
levinsIBM_sim <- function(time,n,m,g,v,sim=5)
{
	da <- data.frame()

	for(i in 1:sim) {
	  
	  pp <- levins_IBM(time,n,m,g,v)
	  
	  da <- rbind(da,data.frame(time=1:time,pob=pp,sim=i,tipo="IBM"))
	}

 	pp <- levins(time,n/v,m,g)*v
	  
  	da <- rbind(da,data.frame(time=1:time,pob=pp,sim=i+1,tipo="det"))

	return(da)
}

La copio en el archivo Meta_fun.r


source("Meta_fun.r")

le <- levinsIBM_sim(500,150,.6,.5,1000,2)
le$tipo <- "0.5"


le1 <- levinsIBM_sim(500,150,.6,.45,1000,2)
le1$tipo <- "0.45"


le <- rbind(le,le1)

le1 <- levinsIBM_sim(500,150,.6,.55,1000,2)
le1$tipo <- "0.55"

le <- rbind(le,le1)

head(le)

g <- ggplot(le,aes(time,pob,colour=as.factor(sim))) + geom_point(size=1) + theme_bw()

g + facet_wrap(~tipo) 

g + geom_line()
  • Graficar solamente 20 años de datos, como en las mariposas. Sería tan fácil distinguir las distintas metapoblaciones?

Referencias

  1. Fronhofer EA, Kubisch A, Hilker FM, Hovestadt T, Poethke HJ (2012) Why are metapopulations so rare? Ecology 93: 1967–1978. doi:10.1890/11-1814.1. https://drive.google.com/file/d/0BzexxHVKtpiATDJ3dlZwSjBtMTA/view?usp=sharing

  2. Black AJ, McKane AJ (2012) Stochastic formulation of ecological models and their applications. Trends Ecol Evol 27: 337–345. doi:10.1016/j.tree.2012.01.014.https://drive.google.com/file/d/0BzexxHVKtpiAY05KZnJpMC10SWM/view?usp=sharing

  3. Ross J V (2006) Stochastic models for mainland-island metapopulations in static and dynamic landscapes. Bull Math Biol 68: 417–449. doi:10.1007/s11538-005-9043-y. https://drive.google.com/file/d/0BzexxHVKtpiAWXNzaFFiMXNabk0/view?usp=sharing

  4. Renshaw E (1993) Modelling biological populations in space and time. Cambridge University Press. Cap 3 https://drive.google.com/file/d/0BzexxHVKtpiAVXczVWJuVEdReHM/view?usp=sharing

  5. Harding KC, McNamara JM (2002) A unifying framework for metapopulation dynamics. Am Nat 160: 173–185. doi:10.1086/341014. https://drive.google.com/file/d/0BzexxHVKtpiAcmNsV3hGNUZOTWc/view?usp=sharing

  6. Henry SM (2009) A Primer of Ecology with R. Springer. https://drive.google.com/file/d/0BzexxHVKtpiAVlhfLWRiS2d4aWM/view?usp=sharing

  7. Crawley MJ (2012) The R Book. 2nd Edition. Wiley. https://drive.google.com/file/d/0BzexxHVKtpiAaGJwMng5WTNveEk/view?usp=sharing

  8. Bolker B (2008) Ecological Models and Data in R. Princeton University Press. https://drive.google.com/file/d/0BzexxHVKtpiAQjhBRDdZQW51WlU/view?usp=sharing

Leave a Comment